TL; DR: Our blog series for complete ABAP beginners. This blog article is for you if you are completely new to ABAP and need some insights into the general logic behind it.
The following exercises will help you understand some basic concepts in ABAP.
“Tell me and I forget, teach me and I may remember, involve me and I learn.”
Benjamin Franklin
On exercism.org you will find 40 ABAP exercises. These are common programming exercises such as Word Count, Tic-Tac-Toe, Scrabble Score and so on that you will probably come across in one way or another when learning a programming language. We recommend that you register there and start doing all these exercises to build up your knowledge of programming and ABAP.
What our blog series Introduction to ABAP will do for you:
- Discuss the task and the considerations you need to make to solve the exercise without having to look up a published solution.
- Randomly show you some ABAP peculiarities that come up in each exercise, so that you understand ABAP better and better.
Learn by example: Prime Factors
https://exercism.org/tracks/abap/exercises/prime-factors
1. The job.
Work out the prime factors of a given natural number.
A prime number is only evenly divisible by itself and 1.
Note that 1 is not a prime number. Some more useful school knowledge: Factors are the numbers you multiply together to get another number. For example: Factor 2 * Factor 3 = 6. “Prime factorisation” is working out which prime numbers can be multiplied together to make the original number.
2. An example to help you understand in depth.
What are the prime factors of 147?
It’s best to start with the smallest prime, which is 2, so let’s see:
Can we divide 147 exactly by 2? 147 ÷ 2 = 73½
No, you can’t. The answer should be an integer, and 73½ is not an integer.
Let’s try the next prime number, 3: 147 ÷ 3 = 49
That worked, now we try to factor 49.
The next prime number, 5, does not work. But 7 does, so we get 49 ÷ 7 = 7.
This is as far as we need to go, because all the factors are prime numbers.
147 = 3 × 7 × 7
Now you have a better understanding of this problem. Have you?
3. What are the constraints of the task?
There is no need to scroll up to see the task again. Here it is:
Calculate the prime factors of a given natural number.
A prime number is only evenly divisible by itself and 1.
Note that 1 is not a prime.
| line of code | constraint | coding |
| 1 | an input (natural number) is given. | input (natural number) |
| 2 | there will be an output of prime factor(s) | output |
| 3 | The smallest prime is 2, that is why we will start prime factorization with divisor 2. | divisor = 2 |
| 4 | How do you get only evenly divisible numbers? Answer: by using the modulo operation (“MOD” or “%” in many programming languages). The modulo operation is the remainder of the division. For example, 5 mod 3 = 2, which means that 2 is the remainder when you divide 5 by 3. If there is a remainder, the number hasn’t been divided equally. For our problem, we would need 5 mod 5 = 0. No remainder, so evenly divisible. More generally: Input MOD divisor < > 0, tells us that the input is not evenly divisible by this divisor and therefore we can’t proceed, we need to change the divisor. | if input MOD divisor < > 0 |
| 5 | We try the next possible divisor, so add 1 to it and try again. | do divisor + 1, start again at line 3 |
| 6 | If input MOD divisor = 0, store divisor as prime factor in our output or in other words: if line 3 of the code is not true (else) store divisor as prime factor in our output | else write divisor as prime factor in our output |
| 7 | Since we have found a prime factor, we can proceed, so we actually divide the given input by the divisor: input = input DIV divisor, starting again with the “new” input at line 3. | input DIV divisor start again at line 3 |
| 8 | When do we need to stop this loop? As you can see, our first input (line 1) is getting smaller and smaller. It has to stop when there is no prime factor left. That is, when the input is equal to 1. Stop this calculation block when the input is 1. Right? If you reverse this constraint: Run as long as input is greater 1. | start again until input > 1 |
Once you understand this, it is actually quite simple. 8 lines of code.
Okay, you’re right, we’re not done yet. Actually, we need 12 lines of code to translate our reflections into ABAP. As you can see here:
4. Our solution translated in ABAP.
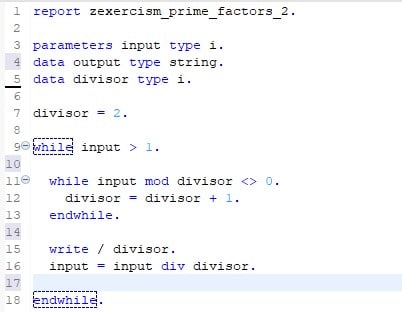
Note: On exercism.org you will find solutions using classes and methods to calculate prime factors. As our blog series is aimed at complete programming beginners, we skipped the object-oriented programming (for now) and wrote a simple ABAP report.
5. Basic ABAP knowledge you need to know to understand the ABAP code above.
ABAP Syntax
Typically, an ABAP statement starts with a keyword and ends with a period. For example:
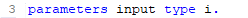
Unlike other languages such as Java or C#, ABAP is not case-sensitive. This means that you can use the ABAP keywords and identifiers in uppercase or lowercase.
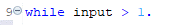
Data declaration
A typical procedural ABAP program consists of type definitions and data declarations. The data declarations describe the data structure that the program uses when it runs.

Parameters are components of a selection screen that are assigned a global elementary data object in the ABAP program and an input field on the selection screen.
So, after running our example. In a SAP GUI system or in eclipse you would have to press F8 to run a program, before you should have saved (Ctrl + s) and activated (Ctrl + F3) your program. After these three steps, you will see that parameters is a data declaration that opens an additional screen (dynpro) in the SAP GUI that receives your input variable.
ABAP has three main types of data: elementary types, complex types and reference types. In our example, only elementary types are used. Therefore, we will only give a brief overview of them in the following table:
| Data Type | Description | Initial Size | Valid Size | Initial Value |
| C | Alphanumeric characters | 1 character | 1 – 65,535 characters | space |
| N | Digits 0-9 | 1 character | 1 – 65,535 characters | Character zero |
| D | Data character YYYYMMDD | 8 characters | 8 characters | Character zeros |
| T | Time character HHMMSS | 8 characters | 8 characters | Character zeros |
| X | Hexadecimal field | 1 byte | 1 – 65,535 bytes | |
| P | Packed Numbers | 8 bytes | 1 – 16 bytes | 0 |
| I | Integers Range 2^31-1 to 2^31 | 4 bytes | 4 bytes | 0 |
| F | 8 bytes | 8 bytes | 0 | |
| STRING | Like C, but has a variable length | |||
| XSTRING | Like X, but has a variable length |
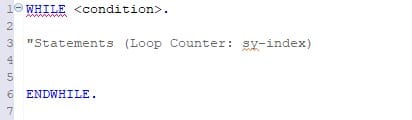
DO/ENDDO and WHILE/ENDWHILE
In ABAP there are two loops that could have helped us solve our prime factor exercise: while/endwhile or do/enddo.
DO/ENDDO: Unconditional and indexed loops:
The block of statements between DO and ENDDO is executed continuously until the loop is exited using exit statements such as EXIT. Specify the maximum number of loop passes, otherwise you may get an infinite loop.
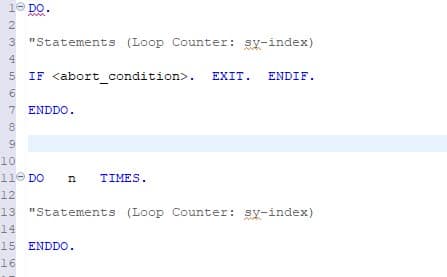
WHILE/ENDWHILE: Header-controlled loops
The statement block between WHILE and ENDWHILE is executed until the specified condition is no longer true. The condition is always checked before the statement block is executed.
WRITE
One of the very basic ABAP statements used to display data on the screen is the WRITE statement.
In our example, the backslash starts a new line for each output number.
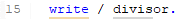

Additional information.
For additional information, see the SAP keyword documentation:
English: https://help.sap.com/doc/abapdocu_752_index_htm/7.52/en-us/abenabap.htm
German: https://help.sap.com/doc/abapdocu_752_index_htm/7.52/de-de/index.htm





