Seit der Vorstellung von ChatGPT vor mittlerweile drei Jahren, sind Machine Learning (ML) und Künstliche Intelligenz (KI) in jeden Bereich der Technologiebranche vorgedrungen. Auch ABAP-Entwickler können dank SAP-Joule ihren Workflow mit Hilfe von KI optimieren, etwa, um automatisch Testklassen generieren zu lassen. Nutzer von On-Premise-Systemen bleiben von diesen Funktionen jedoch bislang ausgeschlossen.
Wer seine eigene KI-Instanz betreiben möchte, braucht dafür schnelle Grafikprozessoren mit viel Arbeitsspeicher. Diese sind nicht nur teuer in der Anschaffung, sondern verursachen auch langfristig hohe Energiekosten. Daher greifen viele Unternehmen auf Cloud-Lösungen zurück.
Doch was ist mit Organisationen, die mit ihrem On-Premise-SAP-System zufrieden sind und trotzdem mit kleineren KI-Modellen experimentieren möchten? Kann man künstliche Intelligenz auch direkt in ABAP programmieren? Die Antwort lautet: Ja. Um diese Möglichkeit zu demonstrieren, habe ich das „Hello World!“ des Machine Learnings in ABAP umgesetzt: eine einfache Handschrifterkennung auf Basis der MNIST-Datenbank. Ich habe mich dabei an der Lösung aus dem LinkedIn Learning Kurs Neuronale Netze in C/C++ von Dr. Gerhard Stein orientiert.
Wie KI funktioniert
Künstliche Neuronale Netze
Auch wenn es den Anschein hat, als sei KI eine ganz neue Entwicklung, ist das zugrunde liegende Prinzip schon seit Jahrzehnten bekannt. Erste Versuche, diese Art von KI zu realisieren, gab es bereits Mitte des 20. Jahrhunderts.
Kernbestandteil von KI-Systemen sind künstlichen neuronalen Netze (KNN). Sie bestehen aus einer Vielzahl von Neuronen, deren Funktionsweise der einer biologischer Nervenzelle nachempfunden ist. Ein solches künstliches Neuron ist in Abbildung 1 dargestellt.
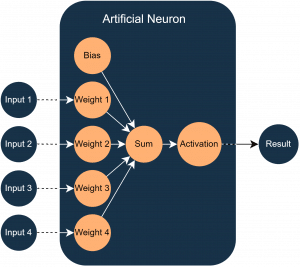
Ein Neuron hat mehrere Eingänge und immer genau einen Ausgang. Die Eingänge laufen im Neuron durch eine Übertragungsfunktion. Dafür wird jeder Eingangswert mit einem individuellen Gewicht multipliziert. Zusätzlich zu diesen Gewichten gibt es einen Bias, der die Flexibilität des Neurons erhöht und es zum Beispiel ermöglicht, auch bei Eingangswerten von null einen Aktivierungswert zu erzeugen. Anschließend werden alle gewichteten Eingabewerte zusammen mit dem Bias aufsummiert. Das Ergebnis dieser Übertragungsfunktion wird dann durch eine Aktivierungsfunktion ausgewertet, die beispielsweise einen Schwellwert definiert, ab dem der Ausgang „aktiv“ wird (also den Wert 1 annimmt).
Werden mehrere solcher Neuronen miteinander verbunden oder verkettet, entsteht so ein künstliches neuronales Netz.
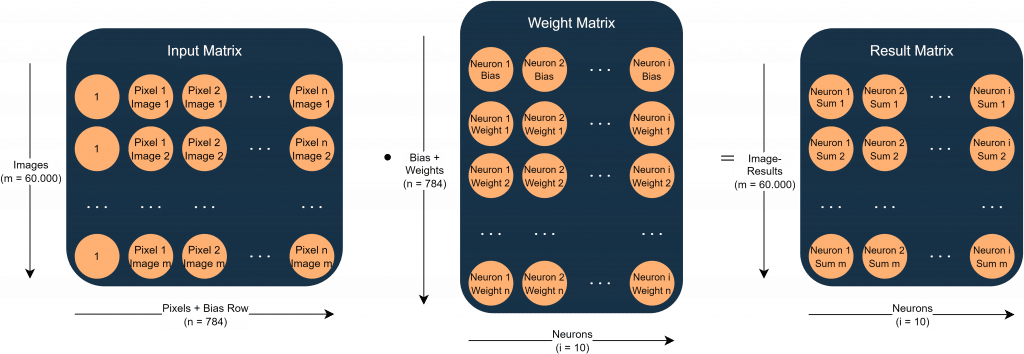
Eine der zentralen Aufgaben bei der Umsetzung ist es, die Funktion eines Neurons mathematisch und programmatisch abzubilden. Hierfür eignet sich die Matrixmultiplikation hervorragend. Die Übertragungsfunktion des Neurons aus Abbildung 1, lässt sich in Matrizenschreibweise wie in Abbildung 2 darstellen:
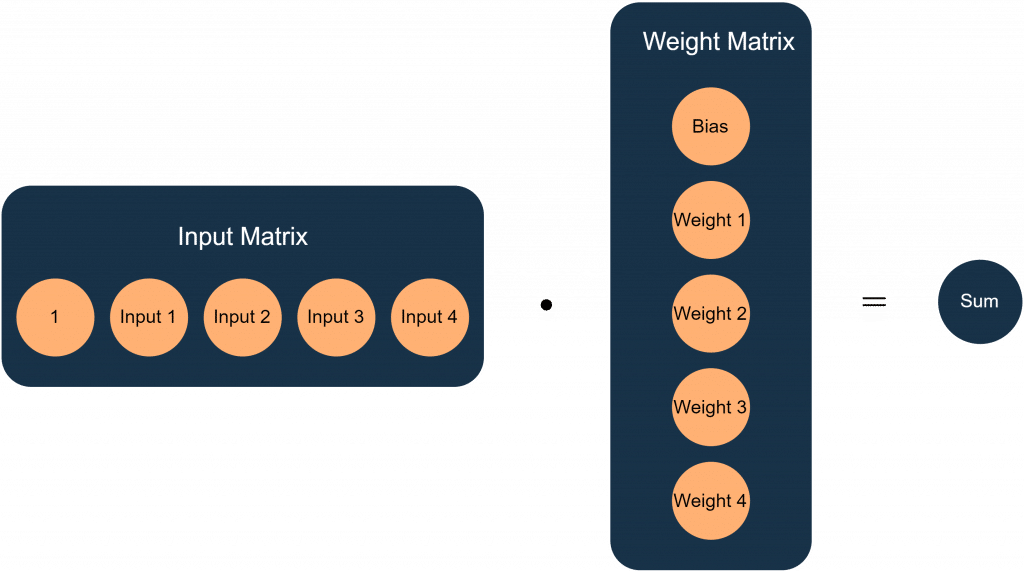
In diesem Fall bilden die Eingänge eine Zeilenmatrix, während die Gewichte eine Spaltenmatrix darstellen. Eine besondere Eigenschaft der Matrixmultiplikation ist, dass sich mit einer einzigen Operation mehrere Ergebnisse gleichzeitig berechnen lassen. Möchte man beispielsweise die Ausgabewerte eines Neurons für mehrere Eingangskombinationen bestimmen, fügt man einfach zusätzliche Zeilen zur Eingangsmatrix hinzu. Analog können mehrere Neuronen berechnet werden, indem man weitere Spalten an die Gewichtsmatrix anhängt. Aus einem einzelnen Ergebniswert entsteht so eine ganze Matrix von Ergebnissen.
Training
Das Ziel des Trainings besteht darin, die Gewichte des Netzes so anzupassen, dass die Ergebnisse möglichst genau den gewünschten Ausgaben entsprechen. Dafür gibt es verschiedene Ansätze. In diesem Beispiel verwenden wir Supervised Learning. Dafür haben wir eine große Liste mit Beispielen für Eingangswerte mit den dazugehörigen gewünschten Ergebnissen.
Im ersten Schritt werden die Gewichte der Neuronen zufällig (innerhalb bestimmter Grenzen) initialisiert. Anschließend wird überprüft, wie gut das Netz die gewünschten Ergebnisse reproduziert. Über eine Verlustfunktion lässt sich der Fehler bestimmen.
Im Trainingsprozess wird dieser Fehler schrittweise minimiert: Ein Gradientenverfahren vergleicht Soll- und Istwerte, und passt die Gewichte so an, dass der Fehler tendenziell kleiner wird. Danach wird das Netz erneut getestet. Dieser Zyklus wiederholt sich so lange, bis die Genauigkeit zufriedenstellend ist. Der Gradient ist die Ableitung der Verlustfunktion.
Da die Menge der Trainingsdaten häufig enorm ist, und die Gewichte nur langsam und vorsichtig angepasst werden, kann dieser Prozess sehr lange dauern. Am Ende des Trainings erhält man eine Menge von Gewichten, mit denen das Netz neue, bislang unbekannte Eingabedaten klassifizieren kann.
Handschrifterkennung mit MNIST-Datenbank
Die MNIST-Datenbank enthält zehntausende Bilder handgeschriebener Ziffern. Zu jedem Bild gibt es ein Label, das angibt, welche Ziffer tatsächlich dargestellt ist. MNIST ist ein Akronym und steht für „Modified National Institute of Standards and Technology“. Der Datensatz ist in 60.000 Trainingsbilder und 10.000 Testbilder unterteilt. Jedes Bild hat eine Auflösung von 28×28 Pixeln, also insgesamt 784 Pixelwerte. Einige Beispielbilder sind in Abbildung 3 zu sehen.
Implementierung des neuronalen Netzes
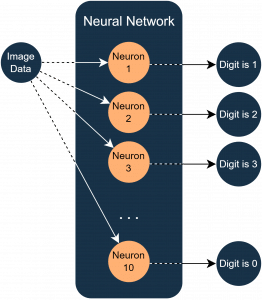
Um alle Ziffern (0–9) erkennen zu können, nutzen wir ein einschichtiges Netz mit Zehn Neuronen – eines für jede Ziffer. Wenn ein Neuron seine Ziffer erkennt, soll es eine 1 ausgeben, ansonsten eine 0.
Die Eingabedaten bestehen aus den Pixelwerten des Bildes (im Bereich 0–255). Diese Werte werden als Eingänge der Neuronen verwendet. Zusätzlich wird ein konstanter Eingangswert von 1 für den Bias ergänzt. Damit ergibt sich eine Gesamtzahl von 785 Eingängen (784 Pixel + 1 Bias). Ein schematischer Überblick ist in Abbildung 4 dargestellt.
Weitere Details
Der Vollständigkeit halber möchte ich an dieser Stelle noch einige technische Details nennen, die zwar für das Grundverständnis nicht zwingend notwendig sind, aber für das Training eine wichtige Rolle spielen:
Als Aktivierungsfunktion wird die Sigmoid-Funktion genutzt. Diese bildet das Ergebnis der Übertragungsfunktion auf einen Bereich von 0 bis 1 ab, wobei eine Summe 0 der Übertragungsfunktion dem Ausgabewert 0,5 entspricht.
Für die Verlustfunktion und die Gradientenfunktion werden logarithmische Varianten verwendet, da diese gut mit der Sigmoid-Aktivierungsfunktion funktionieren.
Trainingsprozess
Beim Training werden allen zehn Neuronen wiederholt alle 60.000 Trainingsbilder „gezeigt“. Nach jeder Trainingsrunde (Iteration) werden die Gewichte mithilfe des Gradientenverfahrens angepasst. Um den Fortschritt zu überwachen, kann der Fehlerwert nach jeder Iteration über die Verlustfunktion ausgegeben werden.
Da wir für die Berechnungen Matrizen nutzen, lässt sich die Übertragungsfunktion aller Neuronen für alle Bilder in einer einzigen Matrixoperation auswerten. Im Anschluss wird die Aktivierungsfunktion auf jedes Element der Ergebnismatrix angewendet. In Abbildung 5 ist die Matrixmultiplikation eines Trainingsschrittes dargestellt.
Wie man anhand der Größen der Matrizen erkennen kann, ist diese Berechnung sehr rechenintensiv und stellt die größte Herausforderung für die Performance des ABAP-Programms dar.
Implementierung in ABAP
Bisher wurde der Prozess allgemein beschrieben, jetzt muss er noch in ABAP umgesetzt werden. Für die Implementierung verwende ich drei Klassen, auf die ich im nächsten Kapitel weiter eingehe:
- Eine Klasse für die Matrizenrechnung,
- Eine Klasse für das Neuronale Netz,
- Eine Klasse für die Verarbeitung der MNIST-Daten.
Matrizenrechnung
Da ABAP keine native Unterstützung für Matrizenrechnung hat, muss diese Funktionalität in einer eigenen Klasse abgebildet werden. Die Matrixmultiplikation ist der ausschlaggebende Faktor für die Performance, also muss hier besonders viel Wert auf eine möglichst effektive Lösung gelegt werden.
Das naheliegendste Äquivalent zur Matrix in ABAP ist die interne Tabelle. Damit lässt sich eine Matrix zwar prinzipiell über zweidimensionale Indizes abbilden (x, y), allerdings ist die zugrunde liegende Datenstruktur dafür nicht optimal geeignet. Interne Tabellen sind in der Regel als verkettete Listen realisiert, und der Zugriff über Indizes ist vergleichsweise teuer.
Es gibt in ABAP leider keine Alternative dazu, aber man kann die Indexzugriffe reduzieren, indem man die Matrix „flachklopft“, also die Zeilen hintereinander in einer eindimensionalen Tabelle speichert.
Eine Alternative zum Zugriff über Indizes ist das ‚loop at‘, allerdings konnte ich damit keine schnellere Umsetzung finden.
Für die Matrizenrechnung habe ich daher die Klasse Z_RW_CL_MATRIX angelegt. Diese hat zwei Attribute:
- die Dimensionen (x, y)
- Matrixdaten in einer internen Tabelle
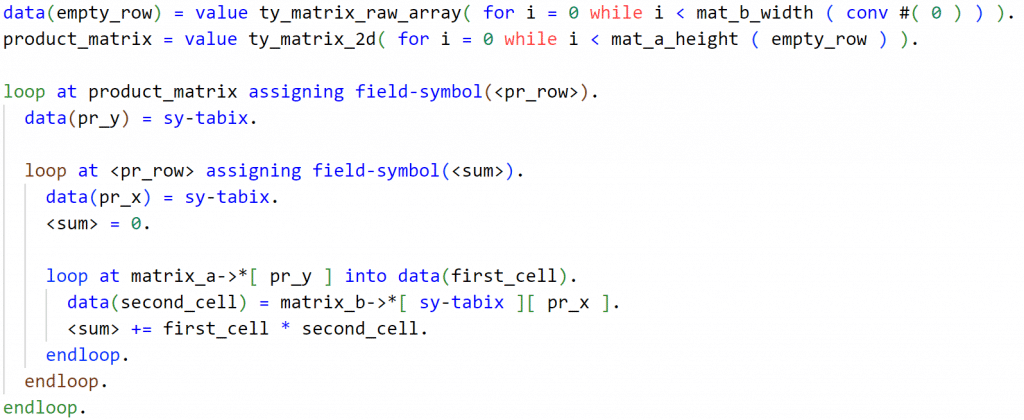
Als Datentyp für die Werte verwende ich „f“, da dieser eine 64-bit Gleitkommazahl darstellt. Das ist ein gängiger Standard im KI-Bereich. Die Alternative “decfloat34“ wäre speicherintensiver und langsamer.
Die statische Methode MATRIX_MULTIPLY nimmt zwei Objekte der Matrixklasse entgegen und gibt das Ergebnis als neues Matrixobjekt zurück. In Abbildung 6 wird der ABAP optimierte Code gezeigt.
Hier sind mehrere Optimierungsansätze umgesetzt:
- • Speicherplatz für Produkt-Matrix wird vorab reserviert (Kein append im loop)
- • Dereferenzierungen von Attributen werden Feldsymbolen zugewiesen
- • Datendeklaration erfolgt außerhalb der Schleifen
- • Matrixdaten sind in einer eindimensionalen internen Tabelle abgelegt
- • Indizes werden akkumuliert anstatt über Koordinaten berechnet
- • Die Summen werden über eine lokale Variable berechnet, um Tabellenzugriffe zu reduzieren
Zum Vergleich zeigt Abbildung 7 meinen ersten Entwurf zur Matrixmultiplikation. Dieser braucht etwa 2,6-mal so lange, wie die optimierte Version.
Wer meinen Blog zu Parallel Processing in ABAP gelesen hat, weiß, dass sich diese Aufgabe hervorragend parallelisieren lässt. Bei großen Matrizen skaliert die Performance nahezu linear mit der Anzahl der Worker Threads. Bei meinem Parallelisierungsansatz werden die Zeilen der Matrix A auf vier Worker-Threads verteilt, um die Berechnung weiter zu beschleunigen.
Das Neuronale Netz
Für die Implementierung der Operationen, die speziell Neuronale Netze betreffen, habe ich die Klasse Z_RW_CL_NET_SINGLE_LAYER angelegt. Es handelt sich dabei um eine abstrakte Klasse, da die Parameter der Neuronen, also Gewichte und Biases, in den Reports als Matrixobjekte gespeichert und dort verwaltet werden.
Die Klasse implementiert folgende private Methoden:
- • SIGMOID – berechnet Aktivierungsfunktion
- • GET_LOSS – berechnet Verlustfunktion
- • GET_GRADIENT – berechnet Gradientenfunktion
- • FORWARD – berechnet aus den Eingabewerten die Ausgabematrix
Zusätzlich implementiert die Klasse das Interface Z_RW_IF_NEURAL_NET, das die zentrale Steuerung des neuronalen Netzes ermöglicht. Es definiert folgende Methoden:
- • TRAIN – startet den Trainingsprozess
- • CLASSIFY – klassifiziert Eingabedaten
- • TEST – führt die Klassifizierung für das gesamte Testdatenset aus und ermittelt die Fehlerrate
Abbildung 8 zeigt den ABAP-Code für die Sigmoid-, Verlust- und Gradientenfunktionen.
MNIST-Datenverarbeitung
Die Bilddaten und Labels der MNIST-Datenbank liegen im CSV-Format vor und können daher problemlos in ABAP eingelesen werden. Jede Zeile der Datei entspricht einem Bild: Der erste Wert ist das Label (eine Ziffer von 0 bis 9), die restlichen 784 Werte sind die Pixelintensitäten (jeweils 0–255).
Für das Einlesen und Aufbereiten der Daten verwende ich die Klasse Z_RW_CL_MNIST. Sie enthält sechs Matrixattribute:
- • M_DIGITS_TRAIN und M_DIGITS_TEST – Eingabedaten für Trainings- bzw. Testset
- • M_LABELS_TRAIN und M_LABELS_TEST – die numerischen Labels aus der CSV-Datei (0–9)
- • M_NEURON_LABELS_TRAIN und M_NEURON_LABELS_TEST – die in One-Hot-Encoding umgewandelten Label-Matrizen für das neuronale Netz (je Neuron eine 1 oder 0)
Der Konstruktor der Klasse kann so parametrisiert werden, dass er nur eines der beiden Datensets lädt. Zudem lässt sich die Datenmenge begrenzen, um die Rechenzeit während der Tests zu verkürzen – insbesondere, da das vollständige Set mit 60.000 Bildern sehr rechenintensiv wäre.
Da die Attribute public read-only deklariert sind, können sie direkt an die Klasse des neuronalen Netzes übergeben werden, etwa zur Durchführung des Trainings oder zur Evaluation auf dem Testdatensatz.
Auswertung der Lösung
Training
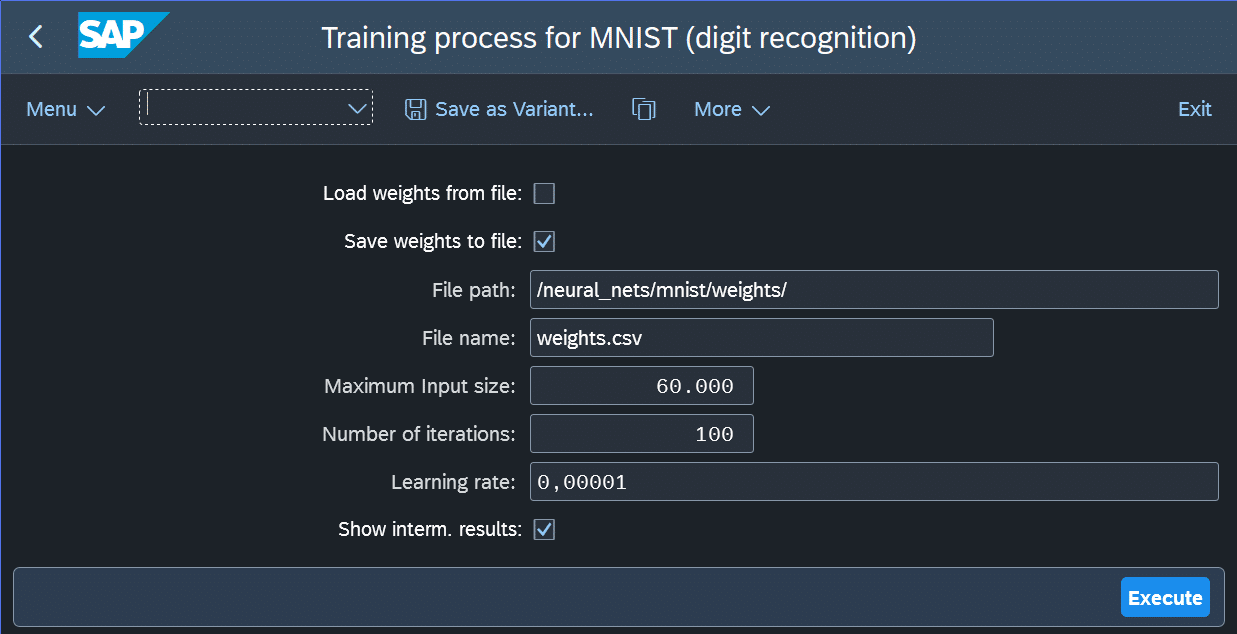
Das Training des neuronalen Netzes kann über einen eigenen Report gestartet werden.
Dieser ist parametrierbar und ermöglicht es, die während des Trainings ermittelten Gewichte als CSV-Datei zu speichern und später wieder zu laden, um das Training fortzusetzen.
Darüber hinaus können Parameter wie Lernrate und Anzahl der Trainingsschritte eingestellt werden.
Die Lernrate steuert, wie stark die Gewichte pro Iteration angepasst werden und beeinflusst damit, wie schnell (und stabil) das Optimum gefunden wird.
Es lohnt sich, mit diesen Werten zu experimentieren, um ein Gefühl dafür zu bekommen, welchen Einfluss sie auf den Trainingsprozess haben. Abbildung 9 zeigt den Selektionsbildschirm des Reports.
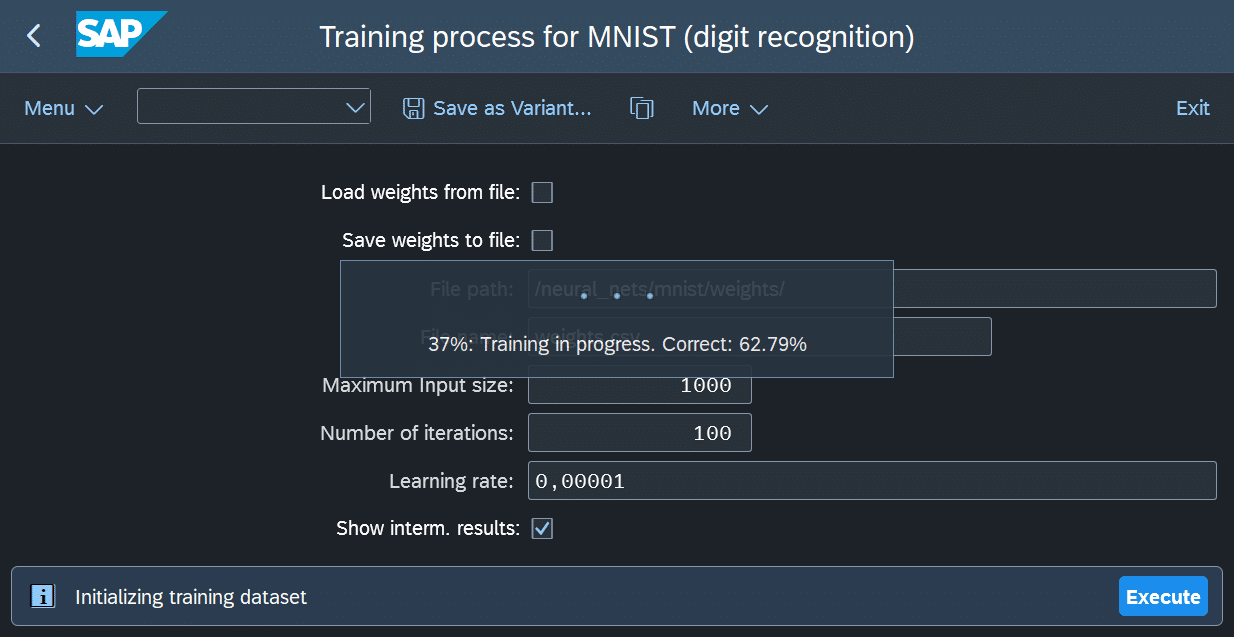
Nach der Parametrierung kann der Trainingsprozess gestartet werden.
Dieser ist rechenintensiv und kann – je nach Anzahl der Iterationen – viel Zeit in Anspruch nehmen. Der Report zeigt während des Trainings regelmäßig Zwischenergebnisse an.
Dabei werden die aktuellen Gewichte mithilfe des Testdatensatzes überprüft, um die Klassifikationsgenauigkeit zu messen. In Abbildung 10 ist ein Beispiel für die Anzeige dieser Zwischenergebnisse zu sehen.
Für längere Trainingsläufe empfiehlt es sich, eine Variante des Reports anzulegen und den Prozess als Hintergrundjob auszuführen. Auf unserem System (eine virtuelle Maschine auf einem Intel-Xeon) dauert das Training mit allen 60.000 Bildern über 100 Iterationen etwa sechs Stunden, trotz Optimierungen und Parallelisierung.
Nach diesen 100 Iterationen erreicht das Netz eine Genauigkeit von rund 90 % auf den Trainingsdaten. Das ist ein realistischer Wert für ein einfaches, einschichtiges neuronales Netz und als Proof of Concept völlig ausreichend, auch wenn komplexere Netze deutlich bessere Resultate erzielen könnten.
Fairerweise muss man anmerken, dass ein neuronales Netz, das immer denselben Wert (z. B. „0“) ausgibt, bei einem gleichmäßig verteilten Datensatz ebenfalls etwa 90 % korrekte Ergebnisse liefern würde. Dieser Wert sollte daher mit Vorsicht interpretiert werden.
Um die Genauigkeit weiter zu steigern, habe ich das Training als periodischen Hintergrundprozess eingeplant, der jede Stunde fünf zusätzliche Iterationen durchführt. Nach etwa einer Woche konnte das Netz so eine Genauigkeit von rund 97 % erreichen, ohne das System dauerhaft auszulasten.
Klassifizierung
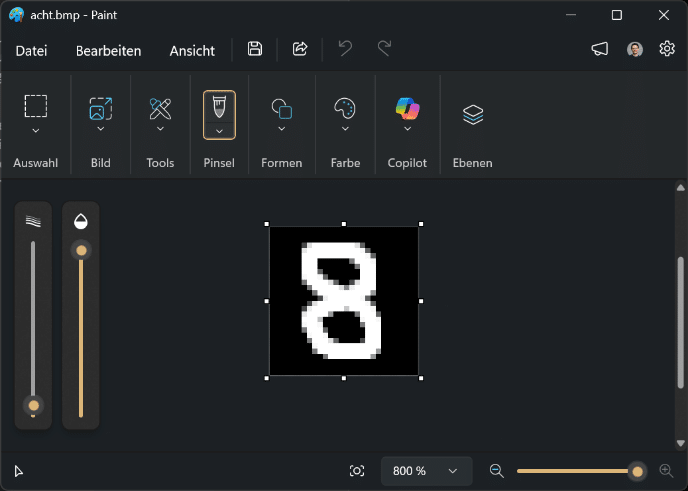
Nach dem Training kann das neuronale Netz zur Ziffernerkennung verwendet werden.
Dafür habe ich einen separaten Report erstellt, über den man eine Bitmap-Datei mit den Maßen 28 × 28 Pixel hochladen kann. Ich habe die Testbilder in MS Paint erstellt, wie in Abbildung 11 zu sehen ist.
Der Klassifizierungsreport gibt anschließend die Ergebnisse der zehn Neuronen aus, also die berechneten Wahrscheinlichkeiten für jede Ziffer, sowie die Laufzeit der Klassifizierung.
Abbildung 12 zeigt den Ergebnisbildschirm.
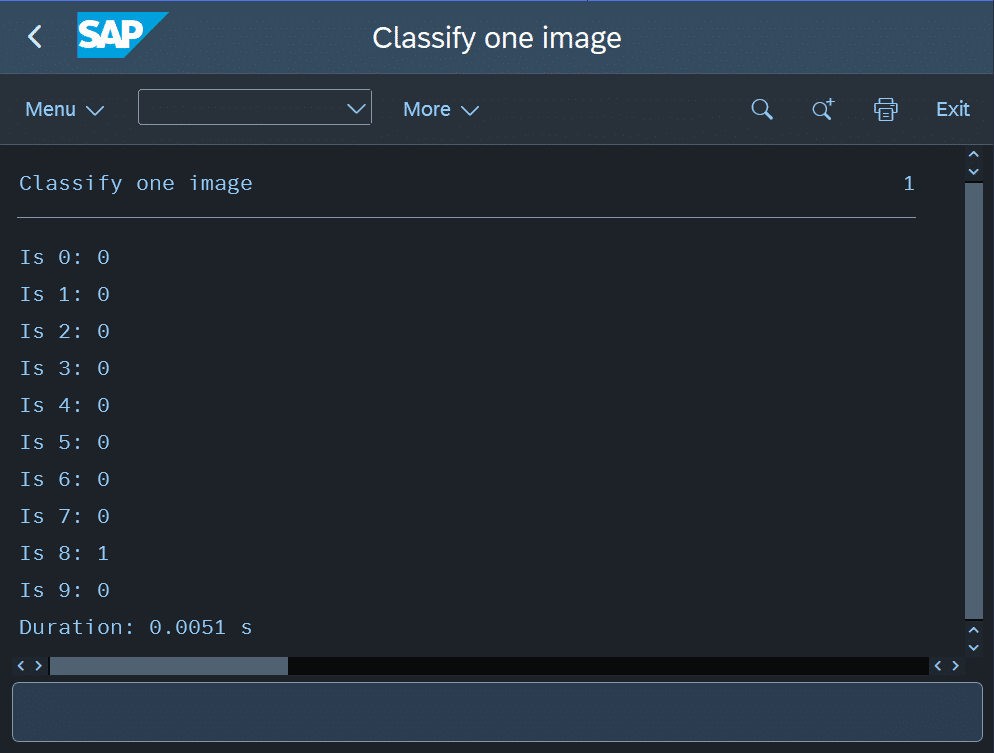
In diesem Test konnte das neuronale Netz die handgezeichnete „8“ korrekt klassifizieren. Ich habe bewusst diese Ziffer gewählt, da sie vom Netz am zuverlässigsten erkannt wird. Bei anderen Ziffern treten trotz einer Gesamtgenauigkeit von rund 97 % noch häufiger Verwechslungen oder uneindeutige Klassifizierungen mit mehreren falschen Positiven auf.
Vermutlich unterscheidet sich meine Handschrift zu stark von den Trainingsdaten, wahrscheinlicher ist jedoch, dass dieses einfache Netz zu wenig Kapazität hat, um zuverlässig zu generalisieren.
Trotzdem betrachte ich das Ergebnis als Erfolg: Der Klassifizierungsprozess funktioniert mit den im Training ermittelten Gewichten vollständig in ABAP, und die Berechnungen laufen korrekt ab, auch wenn das Ergebnis nicht immer stimmt.
Wie der Screenshot zeigt, dauert eine Klassifizierung etwa 5 Millisekunden. Nach dem einmaligen Training ist der Betrieb des Netzes also äußerst schnell, da nur noch ein Durchlauf (Feedforward) erfolgt.
Insgesamt umfasst das Netz 7.850 Parameter (785 Eingänge × 10 Neuronen). Rein theoretisch hochgerechnet würde ein Netz mit einer Milliarde Parametern, also etwa der Größe eines kleinen Large Language Models (LLM), auf demselben System mehrere Minuten pro Durchlauf benötigen, vorausgesetzt, es gäbe genug Arbeitsspeicher.
Das zeigt, warum ABAP trotz aller Optimierungen nicht für moderne KI-Anwendungen wie Bildverarbeitung oder LLMs geeignet ist. Selbst ein kleiner Einplatinenrechner wie der Raspberry Pi würde mithilfe eines Frameworks wie Ollama diese Berechnungen deutlich schneller ausführen.
Fazit
Es ist tatsächlich möglich, neuronale Netze in ABAP zu implementieren und auszuführen.
Die Performance reicht zwar nicht für aktuelle Anwendungen wie komplexe Bilderkennung oder Large Language Models, aber als Proof of Concept zeigt dieses Projekt eindrucksvoll, wie flexibel ABAP sein kann.
Neben der reinen Implementierung spielen auch das Design des Netzes und die Parametrierung des Trainingsprozesses eine entscheidende Rolle. Wer eigene neuronale Netze in ABAP umsetzen möchte, sollte sich daher sowohl mit der Mathematik als auch mit den Performanceaspekten der Programmiersprache intensiv auseinandersetzen.
